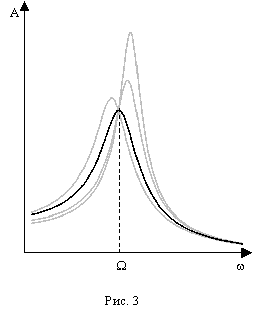
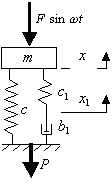
 |
 |
Успешное решение большого количества задач в динамике механических систем [1], связано со знанием фундаментальных свойств систем релаксационного демпфирования [2]. Принципиальной особенностью систем релаксационного демпфирования (СРД) от прочих является существование в их динамических моделях элементов Кельвина или Максвелла [2], т.е. последовательно соединенных демпфера и ослабляющей его действие “релаксационной” пружины (рис. 1, 2). Ее наличие определяется сжимаемостью рабочей жидкости или газа и податливостью элементов конструкции. Любая система релаксационного демпфирования может быть представлена в пространстве различных параметров: при общих значениях жесткости пружины c и массы m релаксационные связи могут быть описаны их жесткостью ci и коэффициентом демпфирования bi. Уравнения движения системы с одной релаксационной связью при динамическом возбуждении массы m силой с постоянной амплитудой F [3] записываются в виде
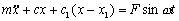
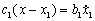
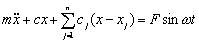
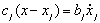
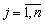
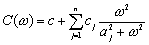
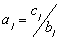находятся два основных и некоторое количество промежуточных участков, близких к горизонтальным. Основные участки расположены в области низких и высоких частот, они равны соответственно статической и "релаксационной" жесткостям системы.
В точке
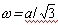находится точка перегиба. 
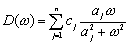имеет экстремальные значения по частоте. Причем положение и величина этих экстремальных значений находится в соответствии
с действительной составляющей. При w ® 0 и w® Ґ величина диссипативной составляющей стремится к нулю. Наличие максимальных значений этой величины позволяет настраивать
устройства такого класса на режимы максимального демпфирования. Максимум демпфирования достигается при w ® a
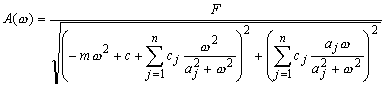
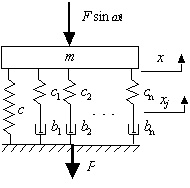
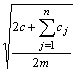(рис. 3), существование которой, в случае модели с двумя и более релаксационными связями, определяется соотношением
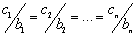Резонансная кривая, максимум которой находится в фиксированной точке, имеет наибольшие диссипативные свойства.
